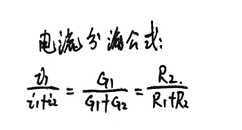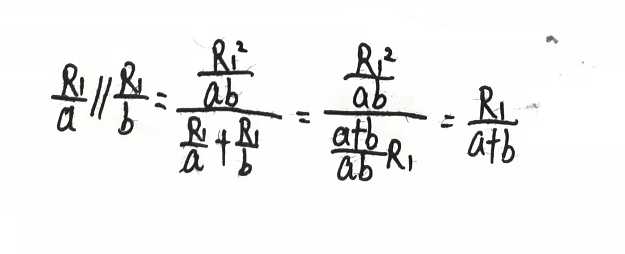本文最后更新于 1202 天前,其中的信息可能已经有所发展或是发生改变。
本章知识网络
2.1 引言
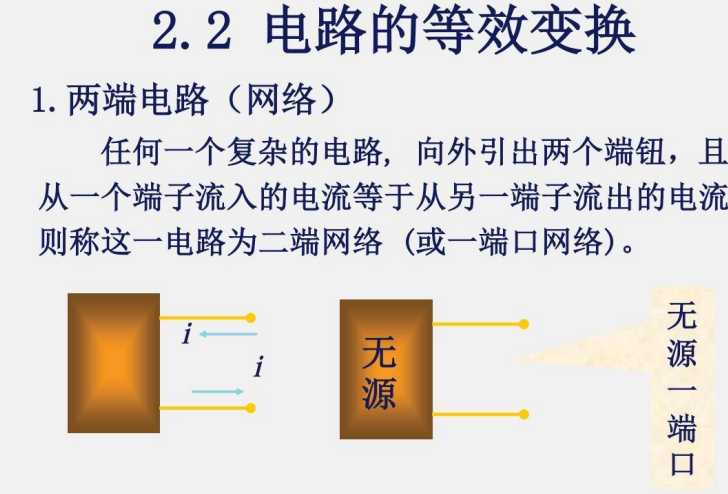
2.2 电路的等效变换
n 端口网络 = 2n 端网络
例如: 3 端口网络,就是 6 端网络
但一般还是用 n 端网络来表示
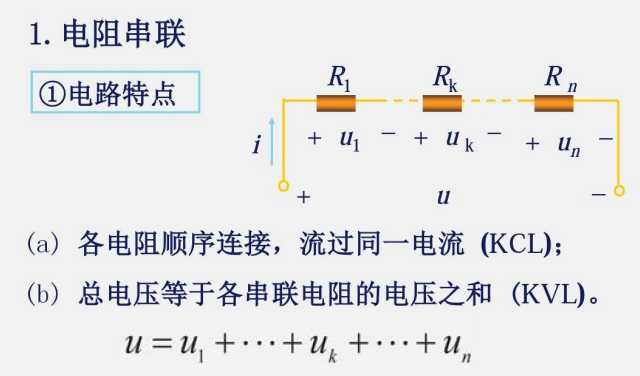
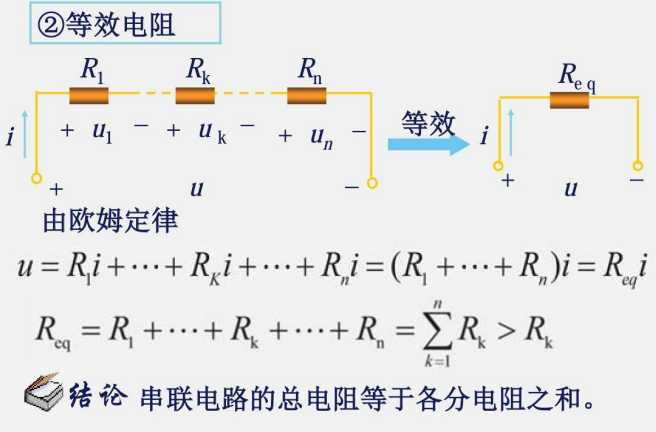
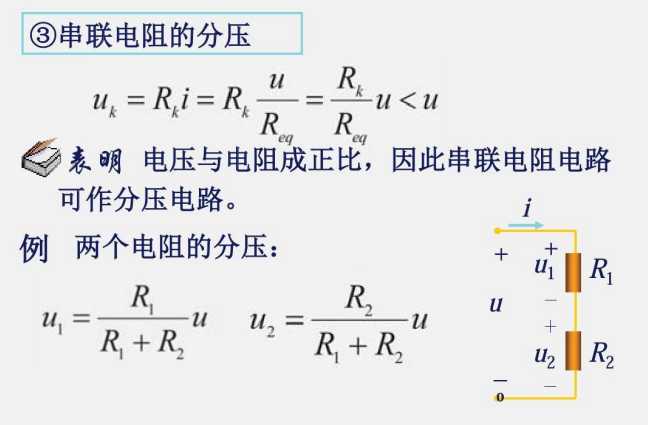
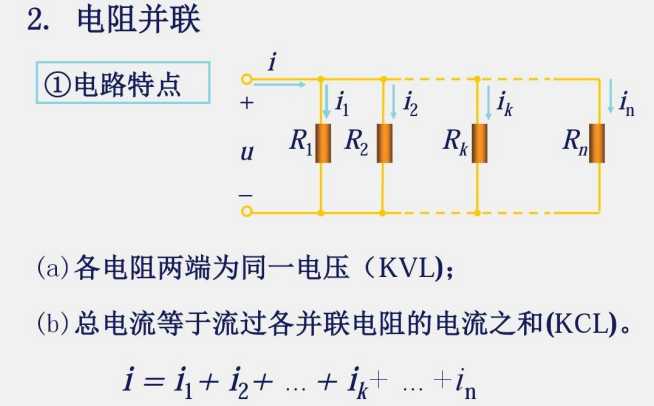
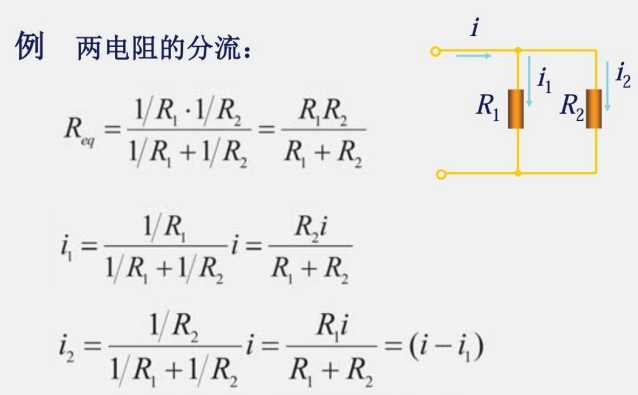
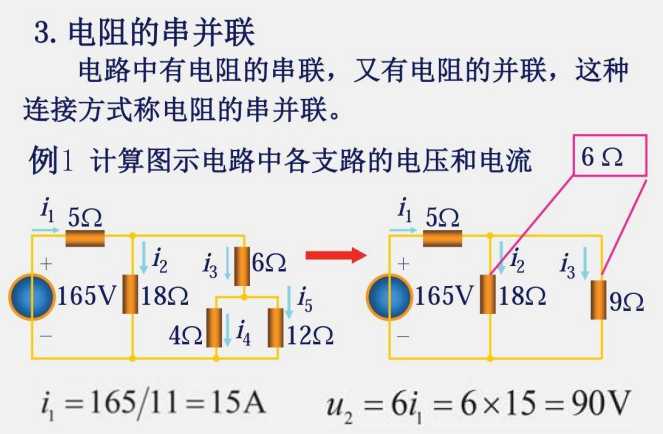
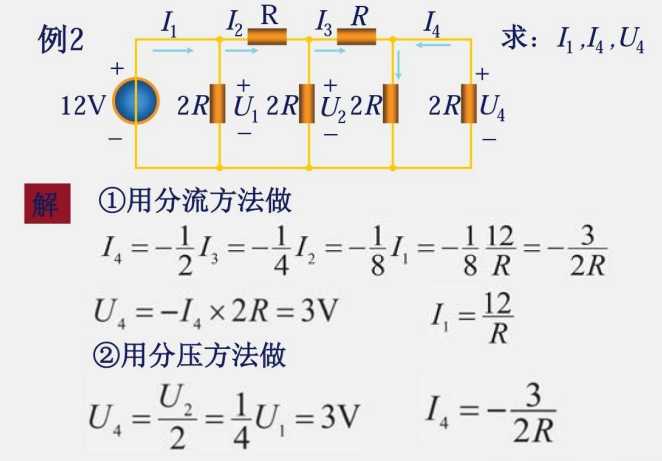
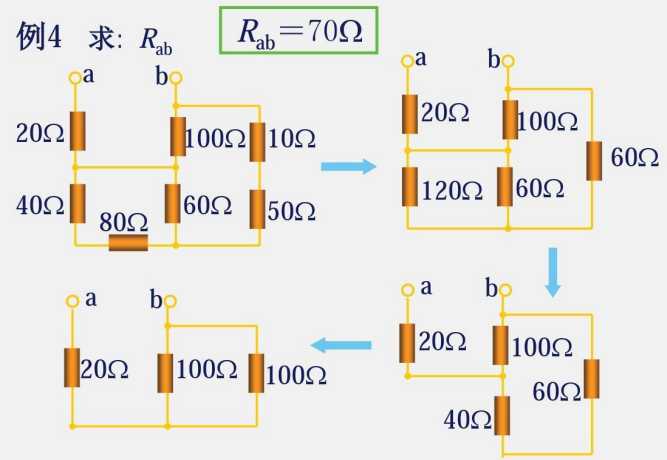
2.3 电阻的串联和并联
电路当中有一些对偶的关系;
电阻-电导
电容-电感
电压-电流
串联-并联
电阻串联用KVL
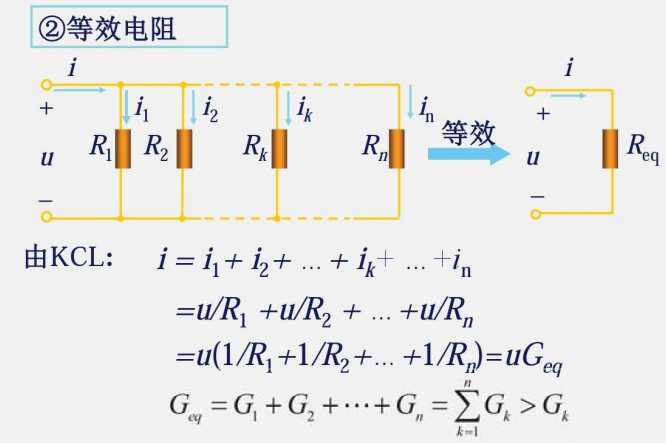
电阻并联用KCL
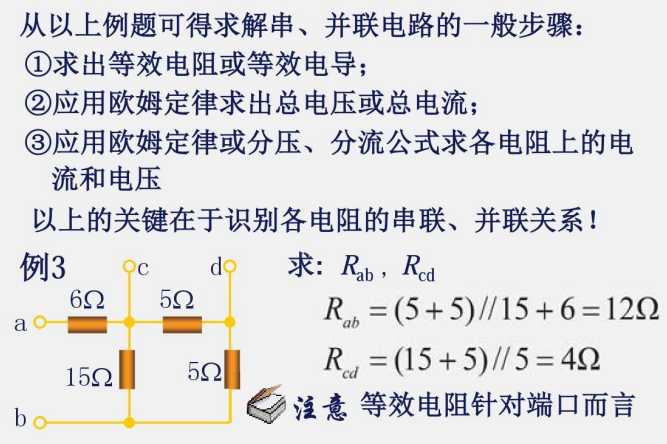
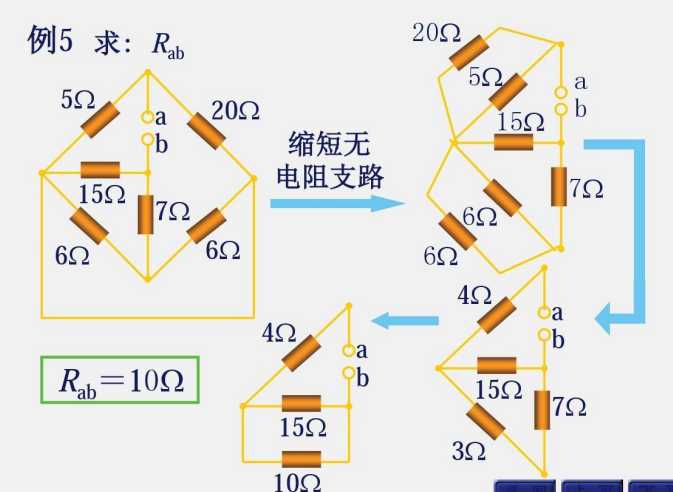
上述题型的变换方法为:把斜的的电阻变换为横平竖直的电阻,然后把跨越的导线结点挪到一起
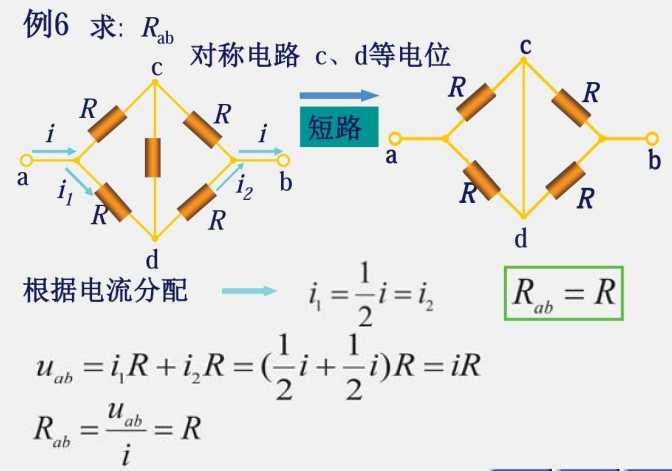
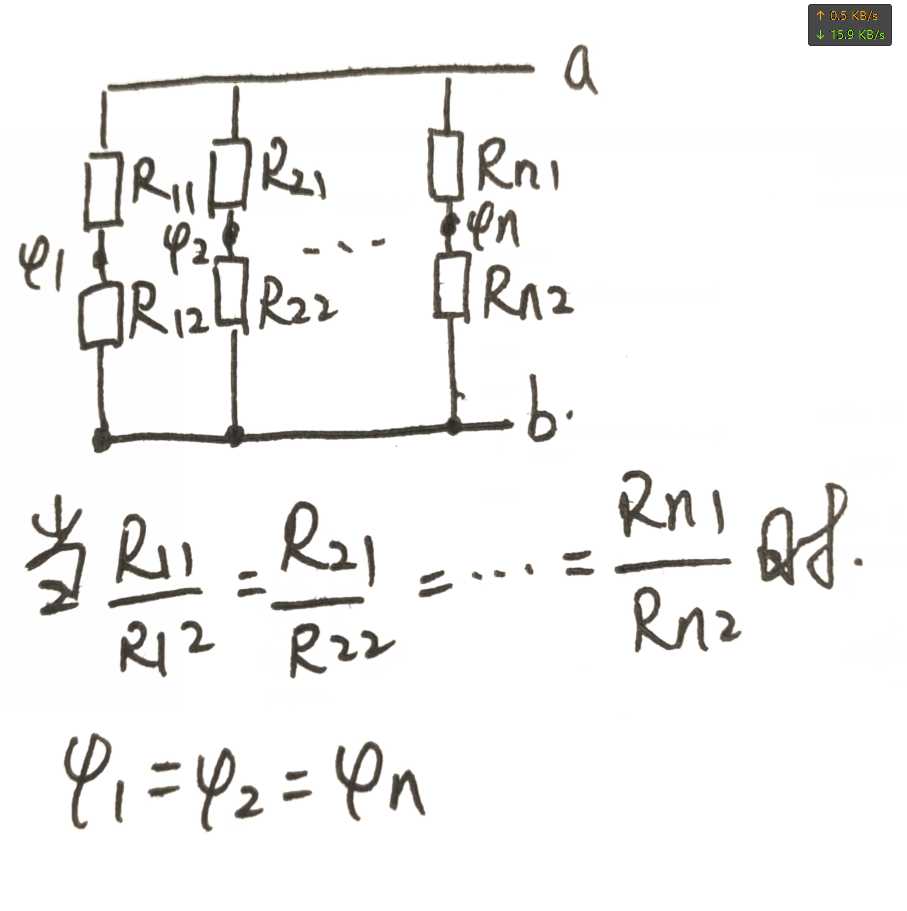
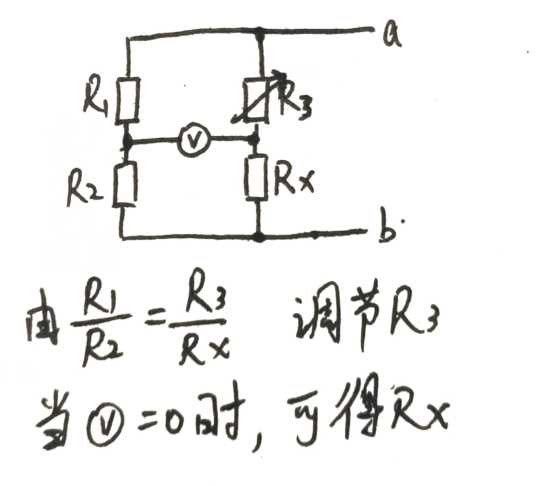
这里需要引入一个电桥的概念
对应这个,可以得出在此电路图中,φc=φd,因此,在 cd 中无论接什么元器件都可以等效成开路或者短路
这个也叫惠思通电桥,这个电桥的结构既不是串联,也不是并联结构
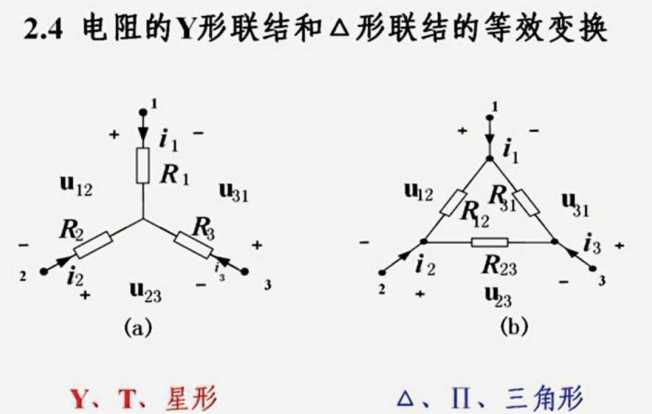
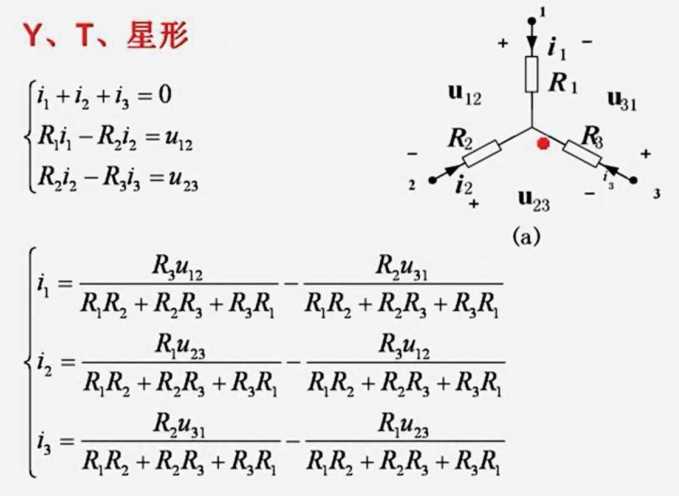
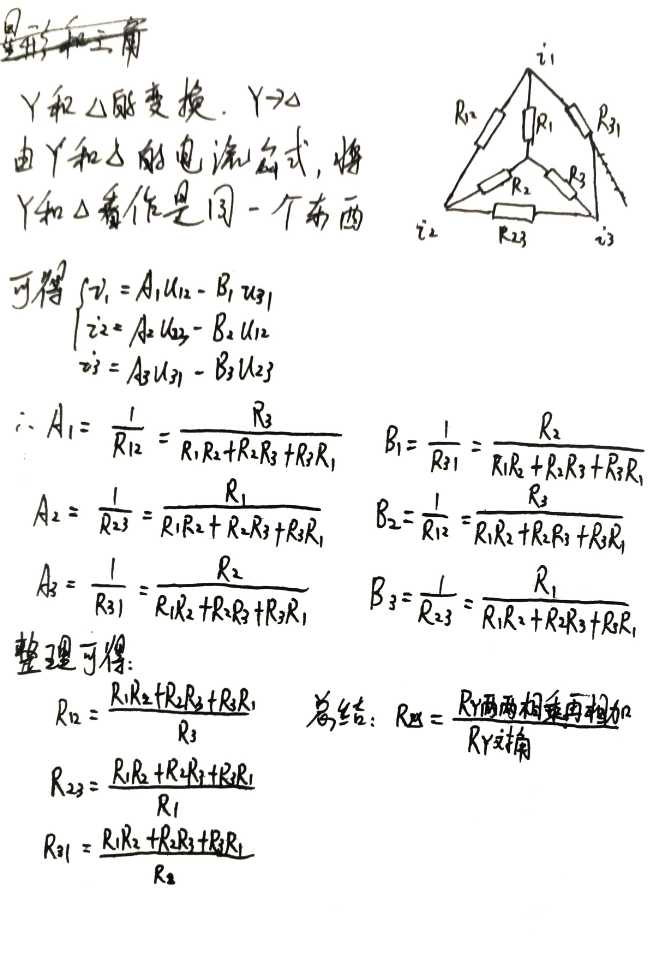
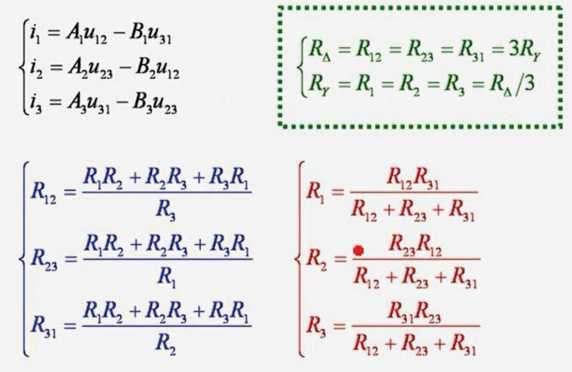
2.4 电阻的三角和星形
三角星形互换
外三内一
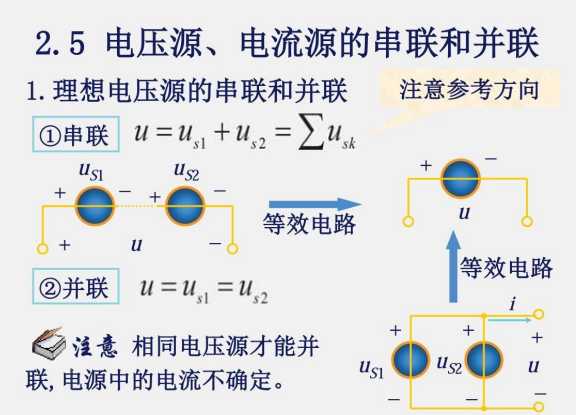
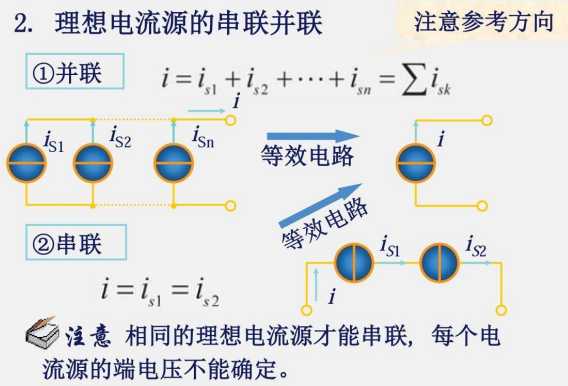
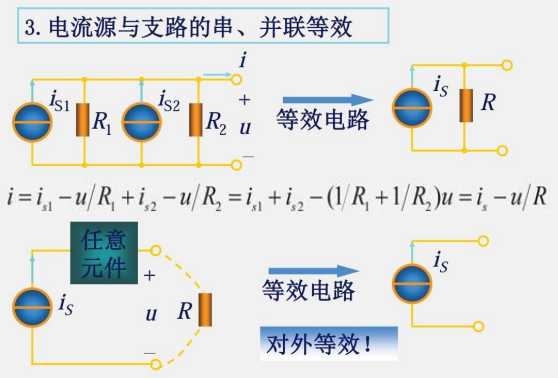
2.5 电压源电流源的串联与并联
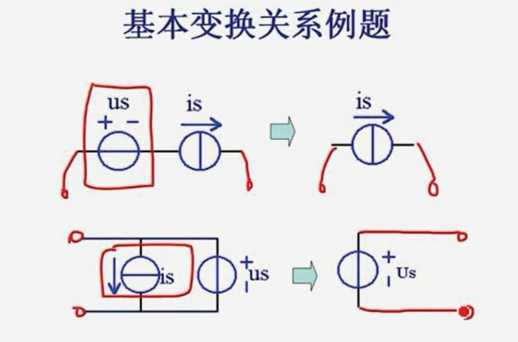
任何元件与电流源串联都等效于只有一个电流源
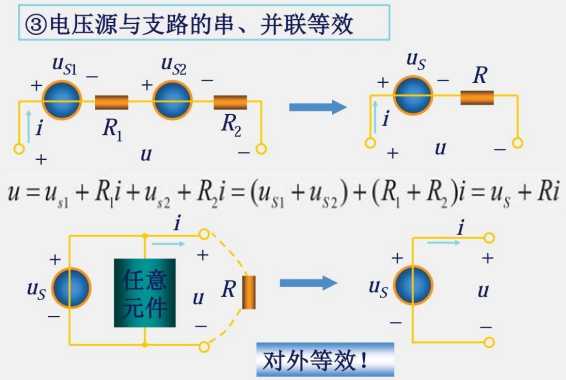
任何元件与电压源并联都等效于只有一个电压源
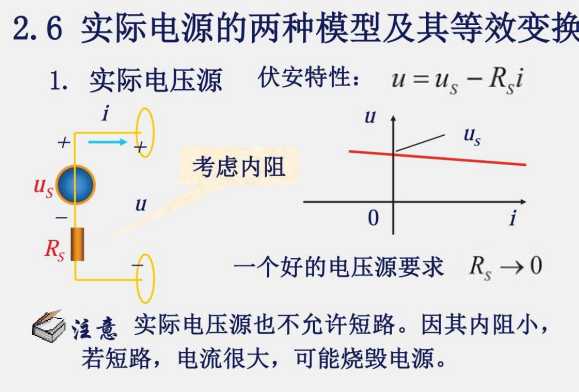
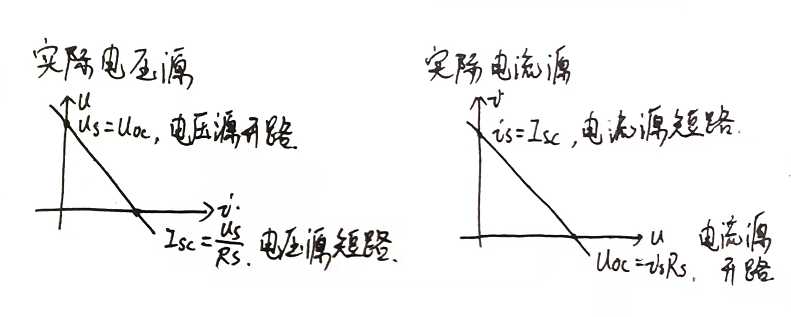
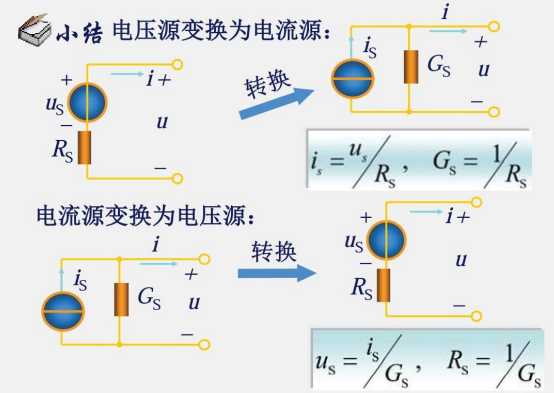
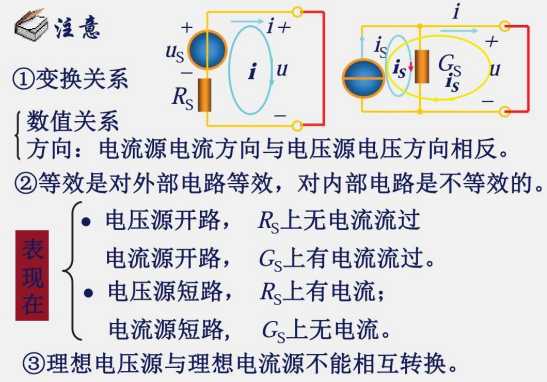
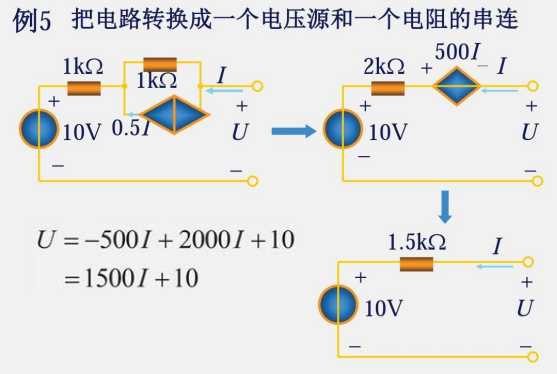
2.6 实际电源的两种模型及其等效变换
由 2.5 可以得知:
电压源并联元器件没有意义,因此实际电压源只能等效成理想电压源与电阻串联
电流源串联元器件没有意义,因此实际电流源只能等效成理想电流源与电阻并联
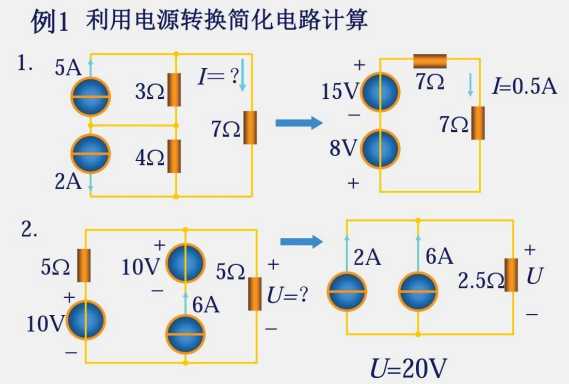
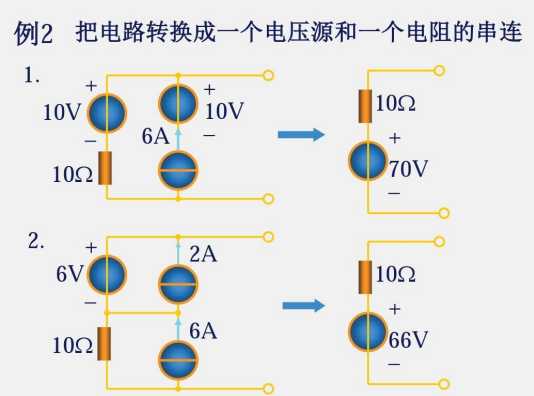
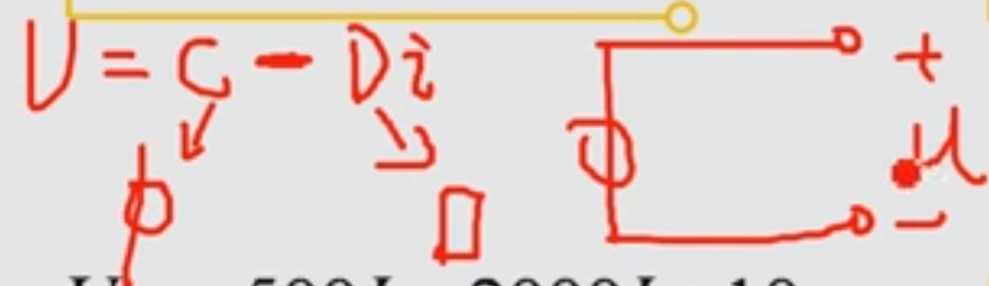
上述方法叫做公式法,不再在原有的元器件上修改,而是在进行初步变换后,一步到位的计算并得出结果
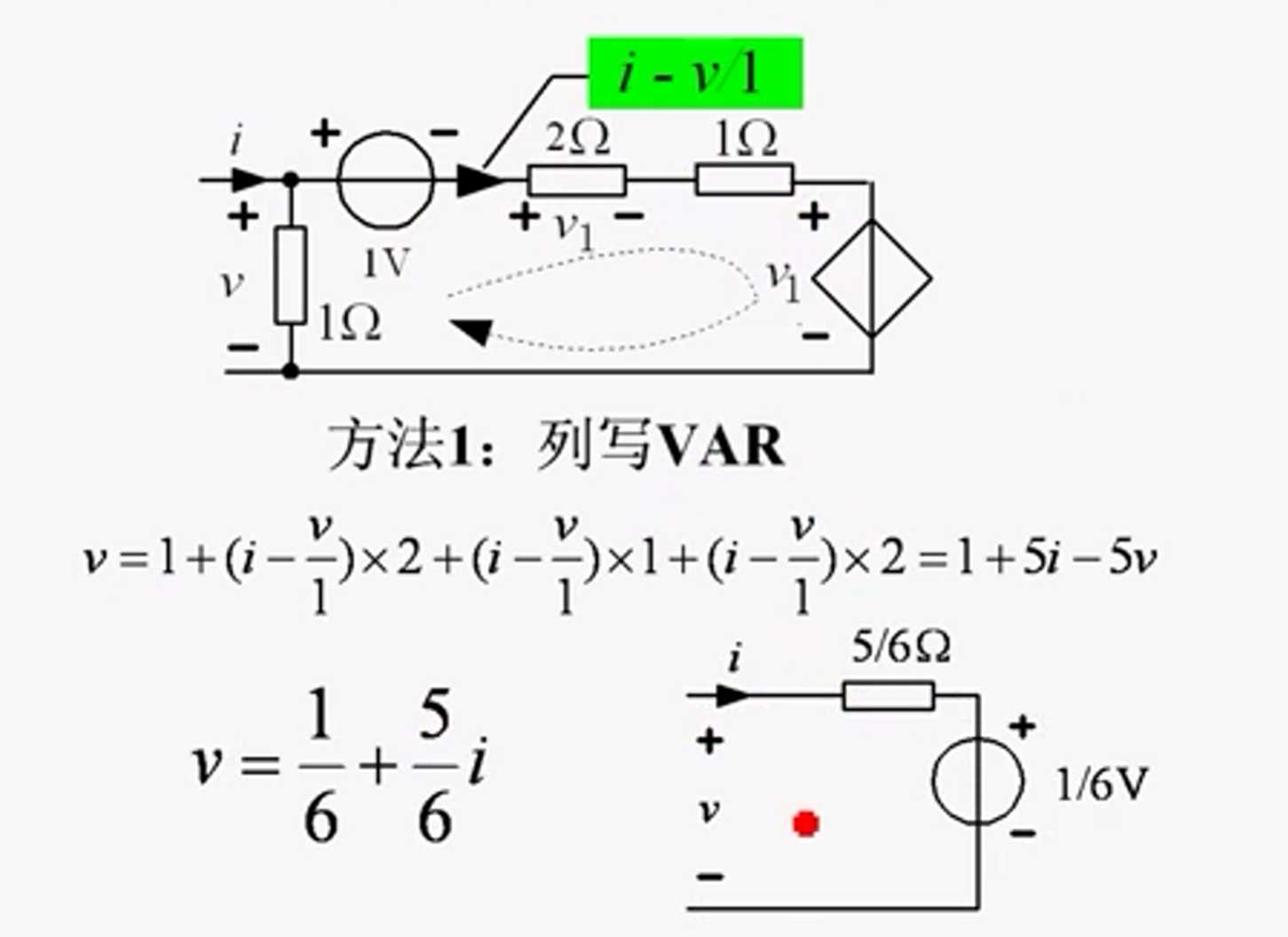
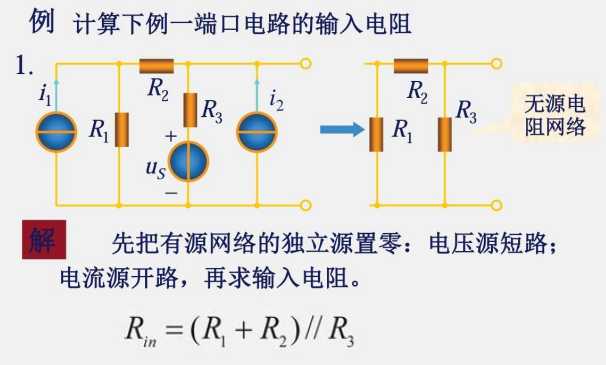
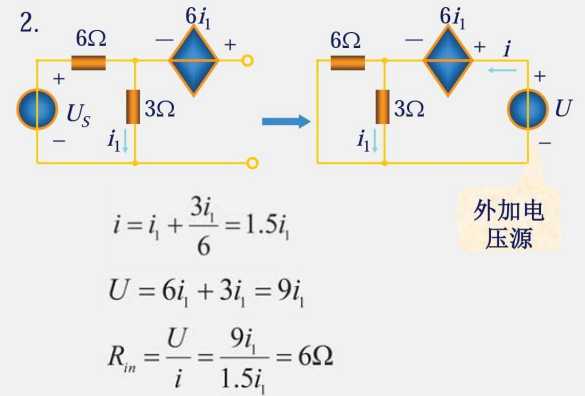
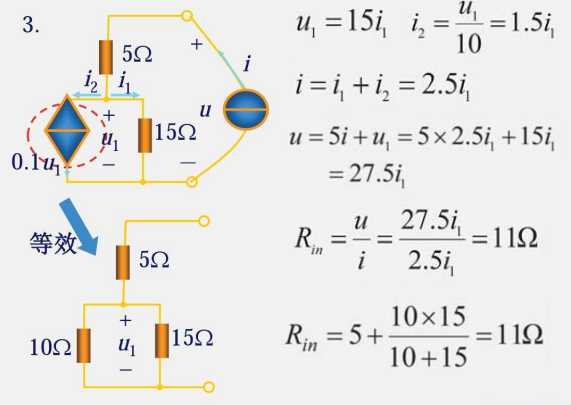
2.7 输入电阻
求输入电阻需要的是一个无源网络,因此需要把独立的电流源和电压源置 0
电压源置零,即电压源电压为 0v,相当于一根导线;
电流源置零,即电流源电流为 0A,相当于开路
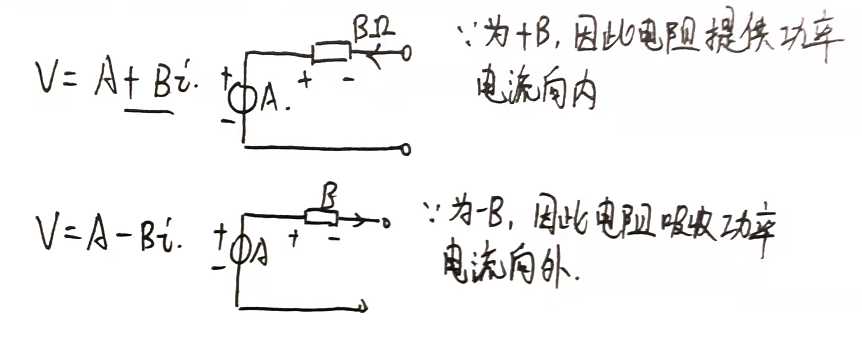
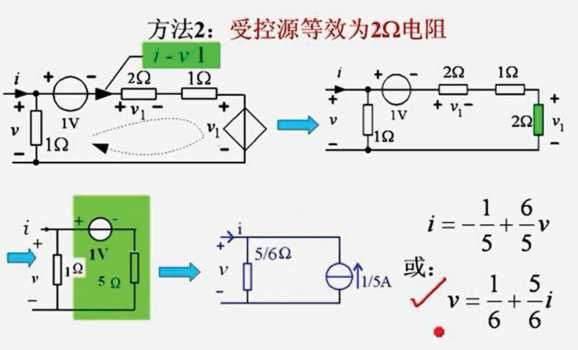
这是要讨论一个阻值为负的东西
此处这个端口网络的阻值为什么,主要看受控源的 u
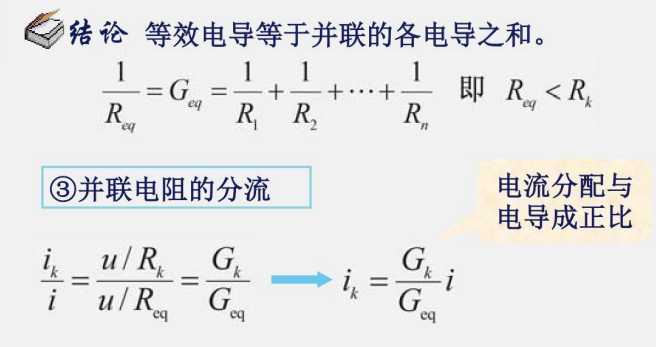
并联公式重要结论
$$
\frac{R1}{a}//\frac{R1}{b}=\frac{R1}{a+b}
$$