本章知识架构

1.1电路和电路模型

输入信号：激励
输出信号：响应

理想电路元件为所有电路元件的最小模型，所有的电路元件都是由理想电路元件组合而成的。

在电路的描述中，统一使用电压源和电流源，不再使用电源、电池等称呼。
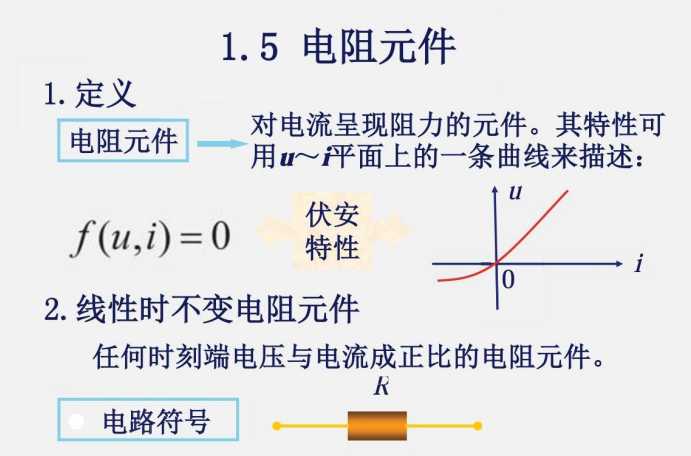
数学描述方式指的是用方程的方式表达电流与电压的关系，例如 f(u,i)=0

例如，灯泡可以等效成相同阻值的电阻。
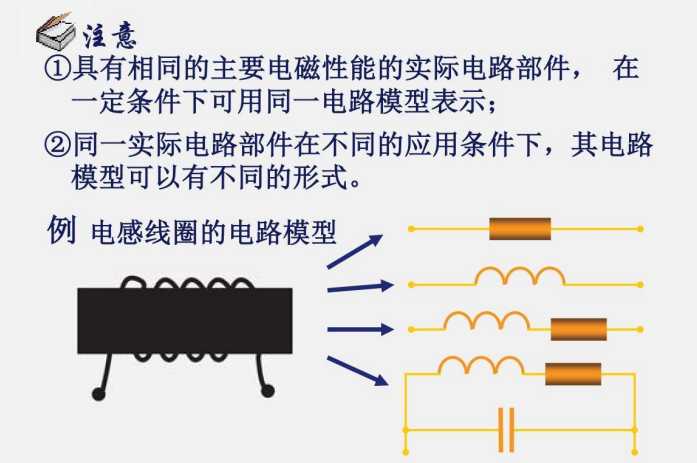
图中的电感，
在通过直流电时，可以等效成一个电阻，这个电阻的阻值为电感线圈的阻值；
在通过交流电时，可以等效成一个无内阻的电感
在通过交流电且考虑功率损耗时，可以等效成一个由电阻的电感；
在通过高频交流电写考虑功率损耗时，可以等效成一个由电阻电感串联再并联一个电容的模型

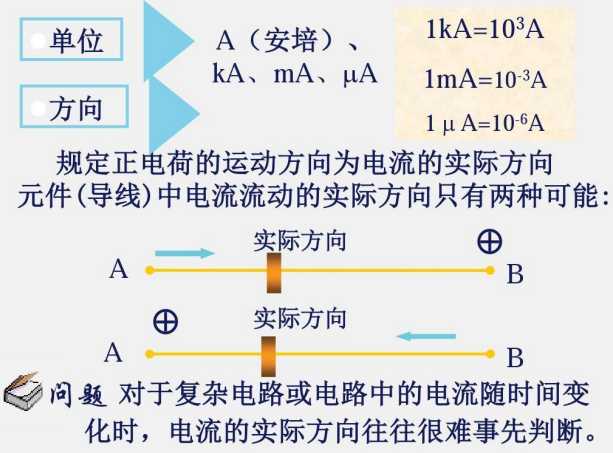
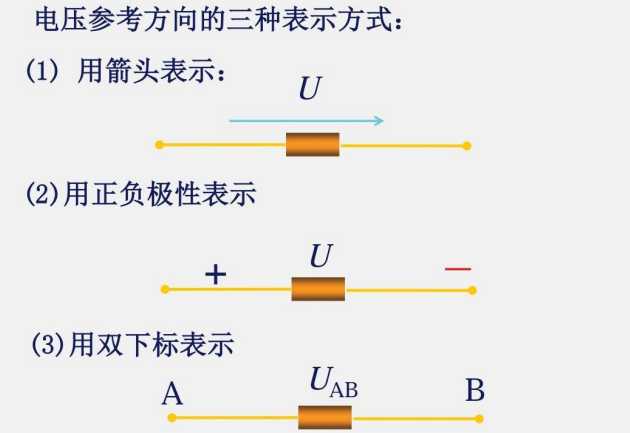
1.2 电流和电压的参考方向

在初高中，电流电压等为大写I、U，指的是恒定值
现在，电流电压等均为小写，i、u，指的是瞬时值
因此，恒定值下的乘法变为了积分，恒定值下的出发变为了求导和微商

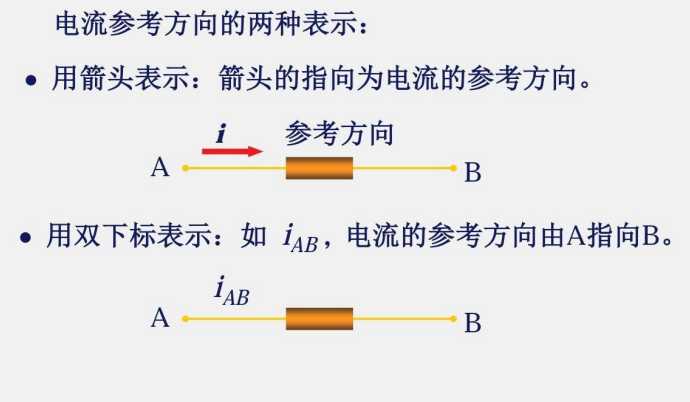
不建议使用双下标法

避免混淆电流参考方向，因此一般情况下只用正负极性表示

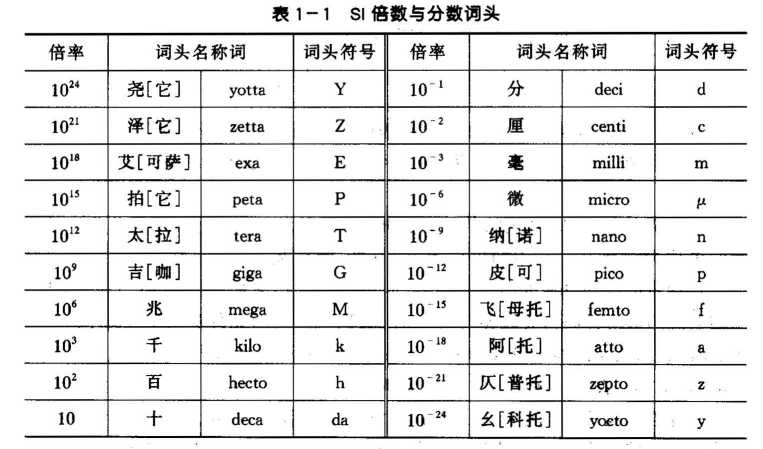
常用的为 T-p

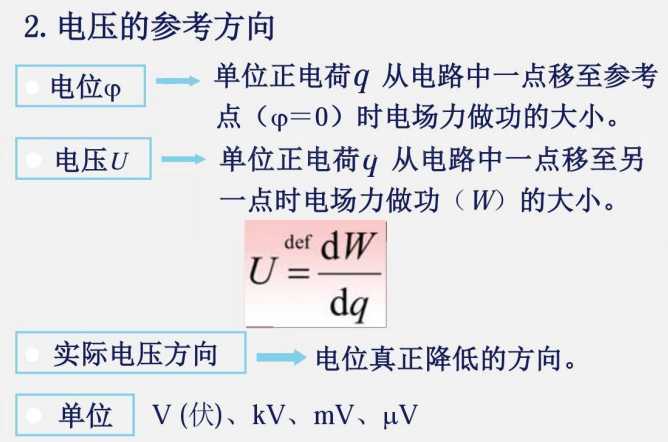
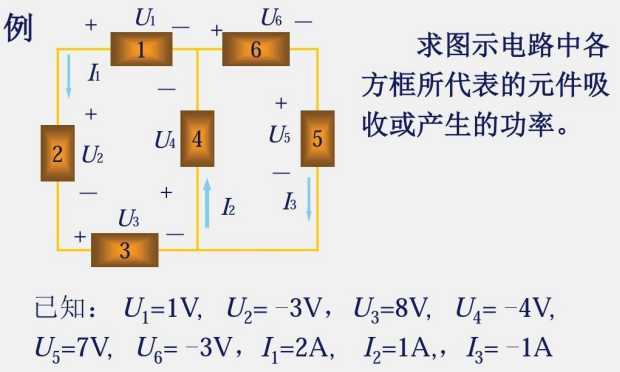
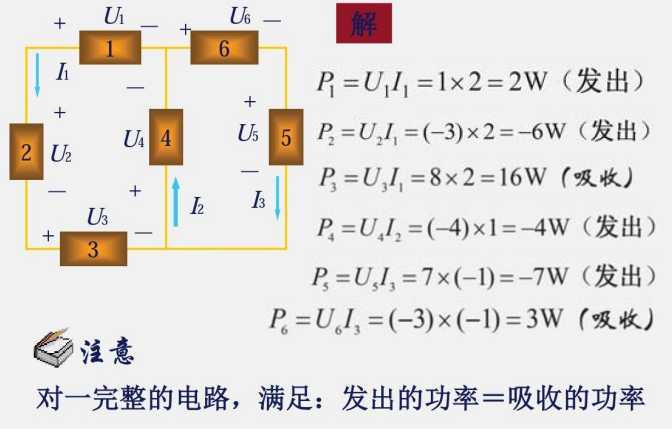
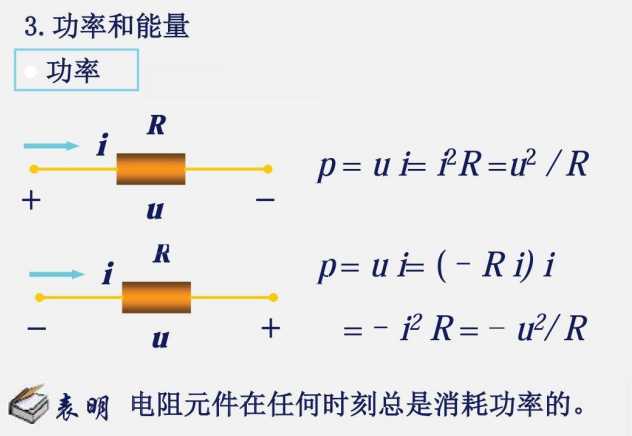
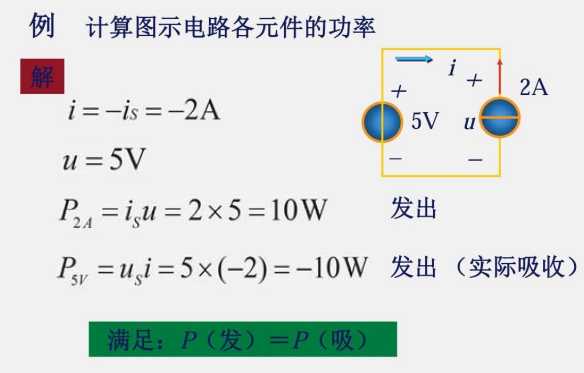
1.3 电功率和能量

口诀：
吸收：+ ；发出：- ；
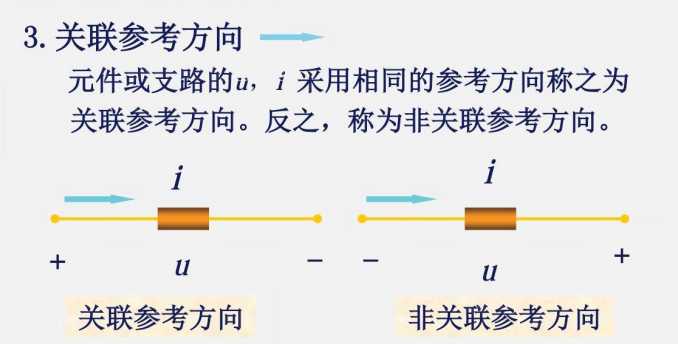
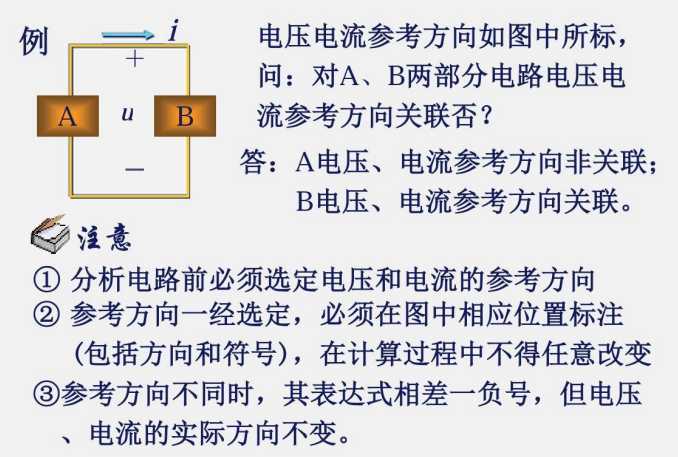
关联：+ ；非关联：- ；
然后直接把正负带入到 P=(符号)(符号)ui 当中；其中 u,i 也需要带符号带入；

在 P=(符号)(符号)ui 中，先确定是否为关联参考方向，然后往 (符号)(符号) 为 + 去凑。所得结果为正数，则为该方式；所得结果为负数，则为另一种方式。
如：在关联参考方向下（+），取吸收功率（+），得出 P>0，则吸收 P；得出 P<0，则发出 -P

1.4 电路元件

其中，d 为电路元件尺寸，λ 为电磁过程的波长
那么把 d 和 λ 同时除以光速 c ，可以得到

$$
\frac{d}{c}<<\frac{\lambda}{c}=\tau <<T，
$$

其中，τ 为电流经过电路元件的时间，T 为电磁过程的周期

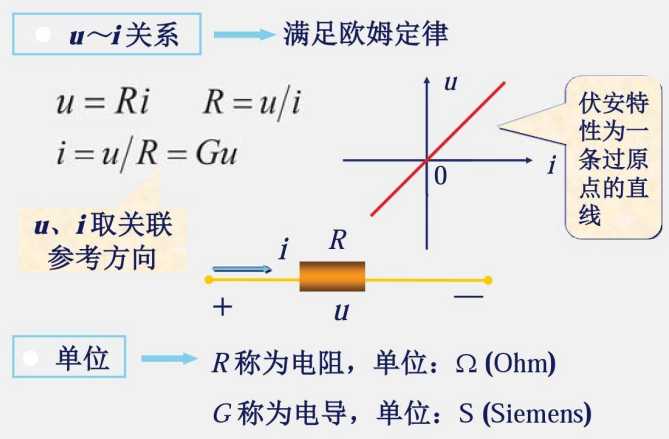
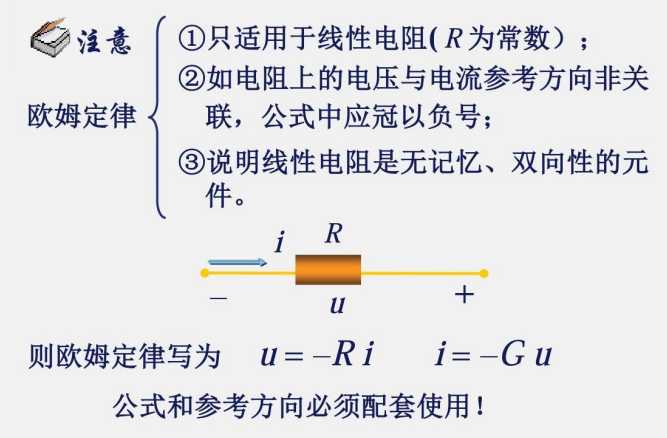
1.5 电阻元件

$$
R=\frac{1}{G}
$$

这是电导与电阻的关系，很显而易见，导就是导通，阻就是阻碍。
当电阻趋于 0 的时候，电导趋于 ∞。

做的功：W=uit
产的热：Q=i^2 ·Rt
无意义：u^2/R·t
当一个东西 W=Q 时，那么这个东西就一定符合欧姆定律

世界上，没有电阻为 0 的阻值，但是由阻值 <=0 的电阻，例如电池

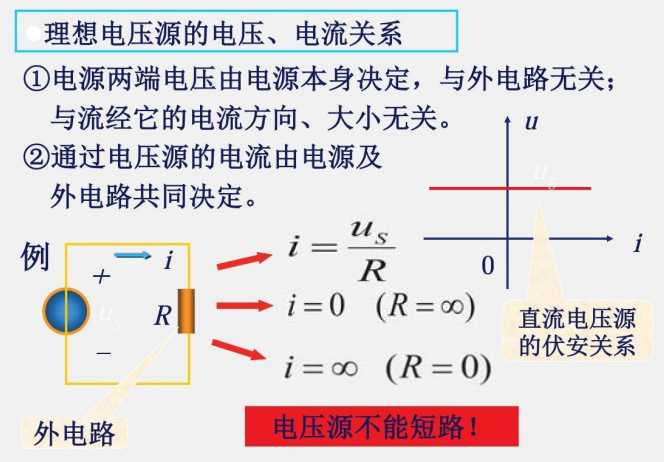
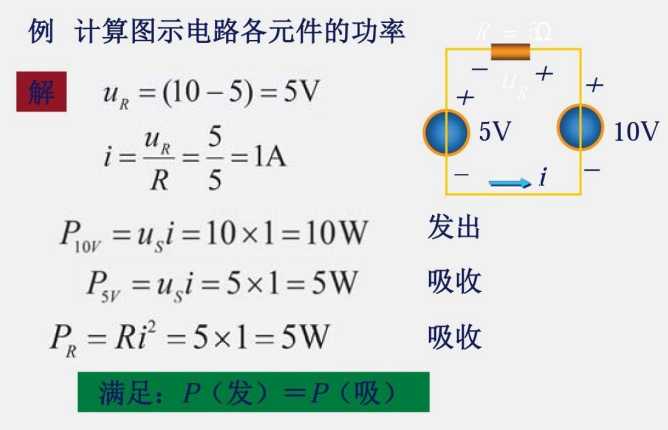
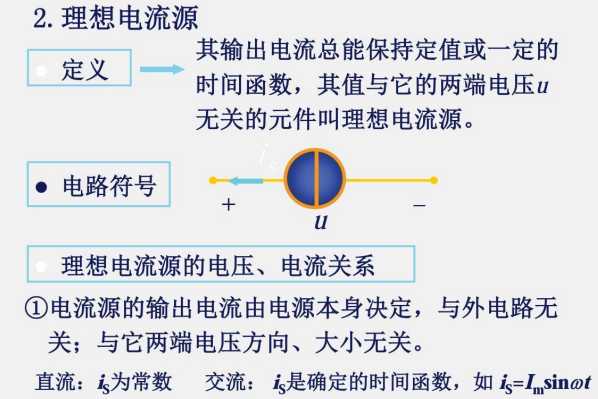
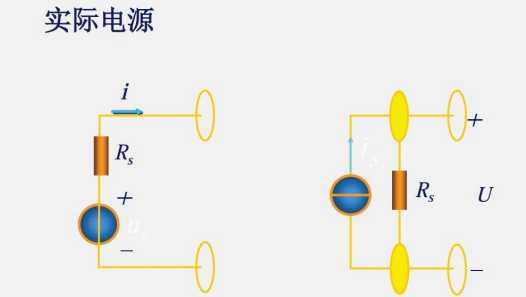
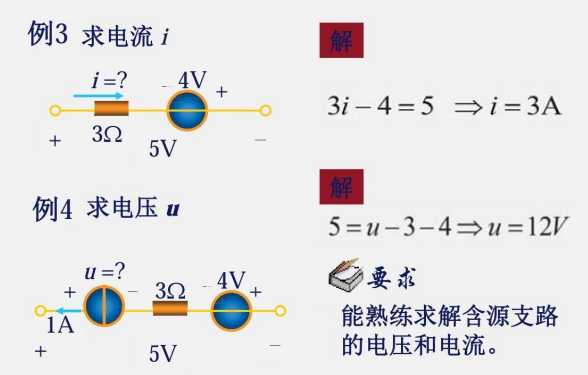
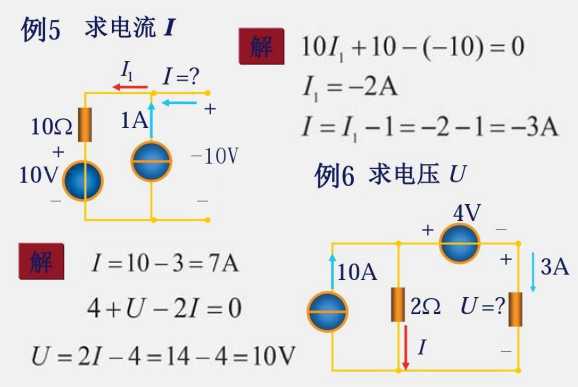
1.6 电压源与电流源

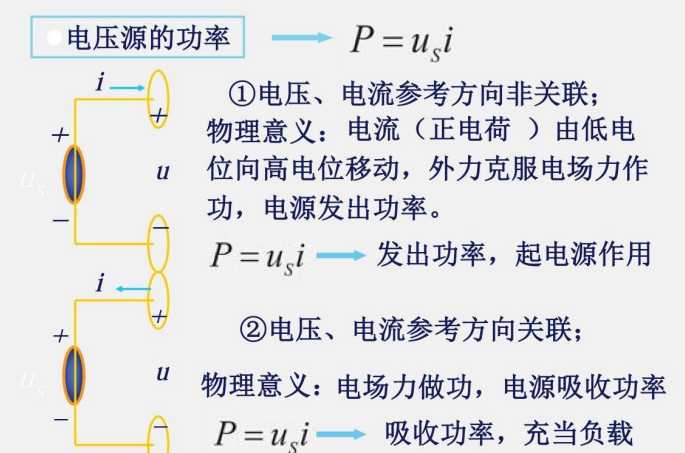
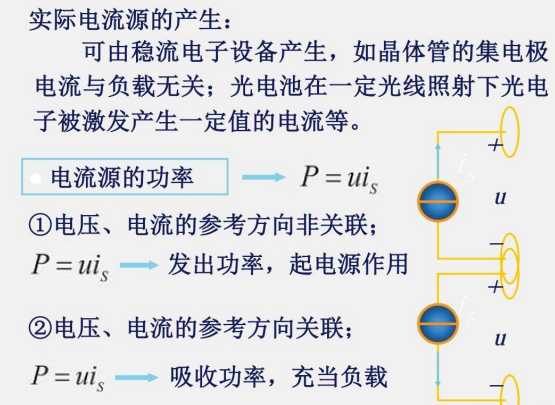
电源既可以发出功率，也可以吸收功率。
当发出功率的时候，就是一个电源，类似于电池放电；当吸收功率的时候就是一个负载，类似于电池充电。

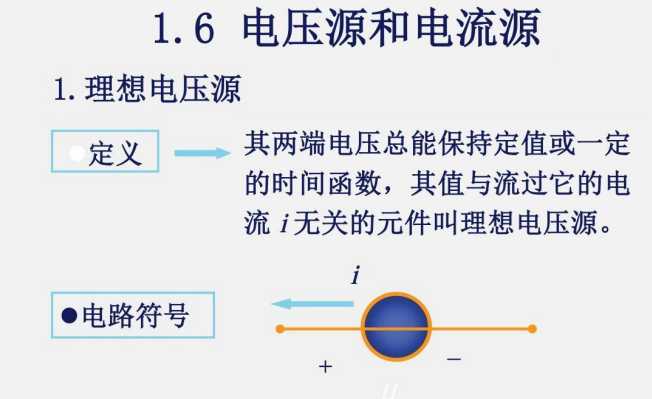
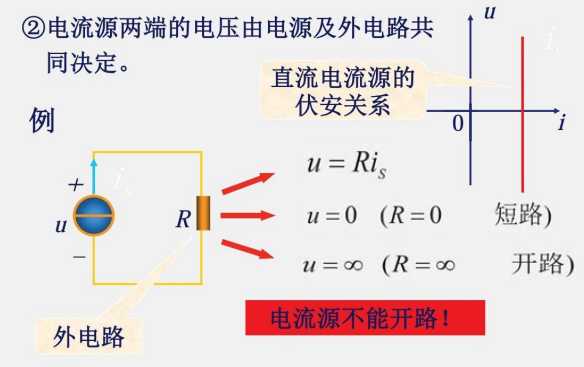
当 i=∞，电压源会损坏

电流源不能开路，就像有人想要打喷嚏，但非要捂住嘴巴不打
电流源不能串联，特别是输出电流不一样的电流源，串联必定会导致其中一个损坏

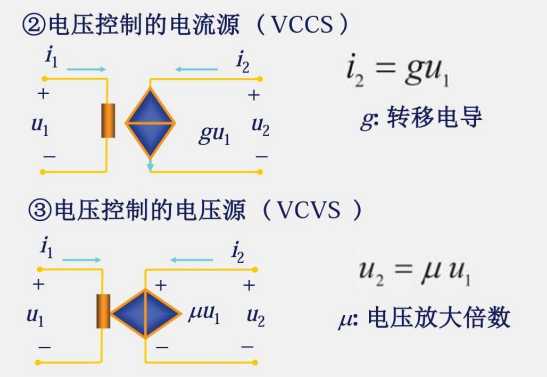
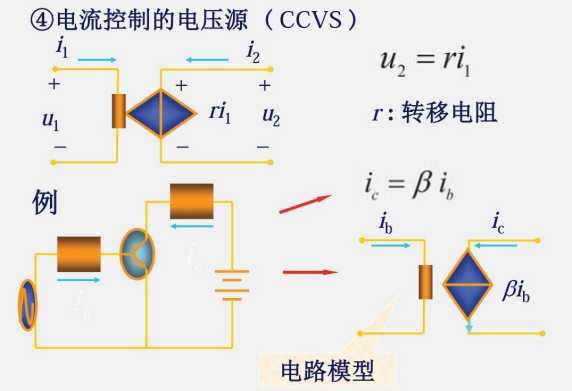
1.7 受控电源

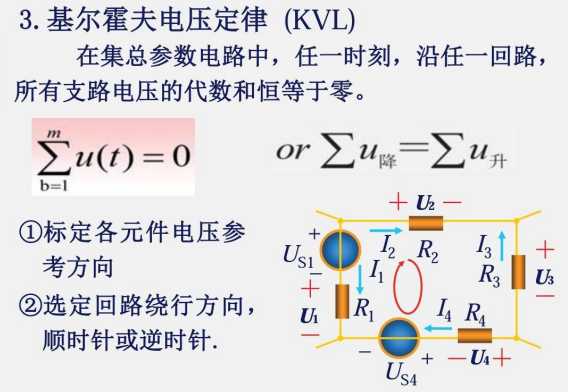
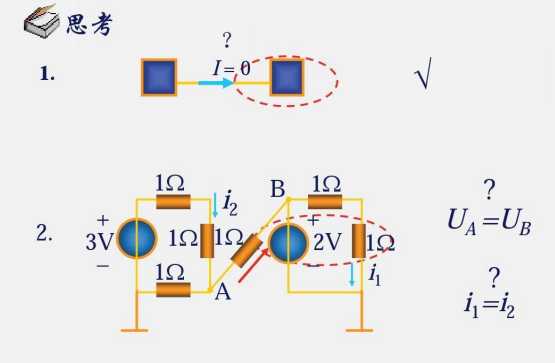
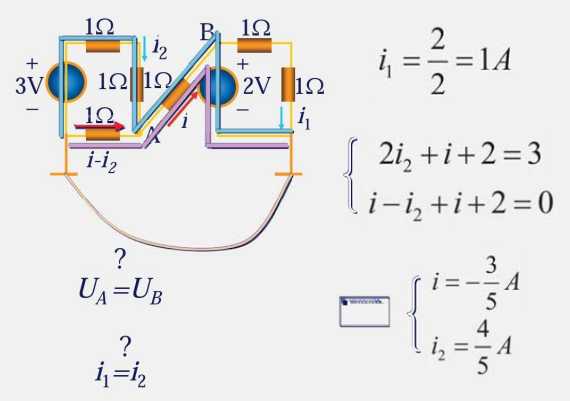
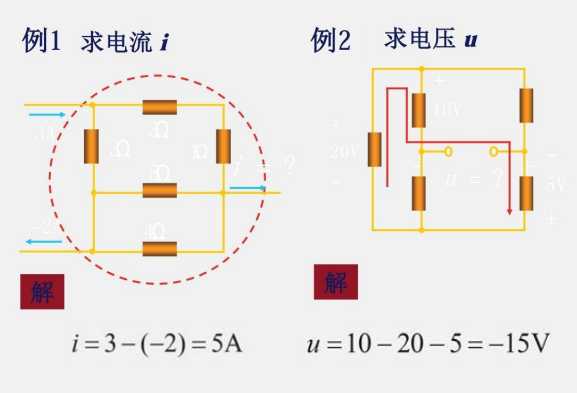
1.8 基尔霍夫定律

通常来说，把串联在一起的元器件称为一条回路，方便分析与计算
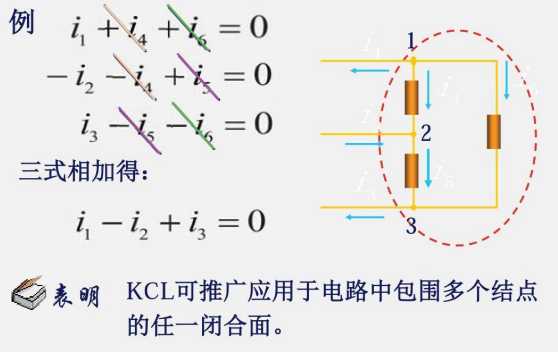
同理，把并联在一起的元器件称为一个结点（三条或以上支路的连接点）

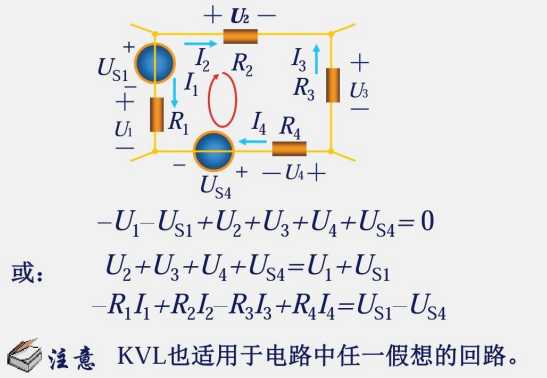
图中有两个网孔

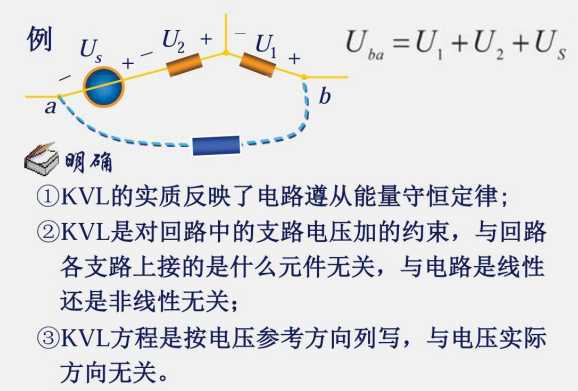
此处很明显的可以看出点位 b 高于 a，因此这个假设的电阻的电位右高左低。
再假设电流方向为逆时针方向